forward-kinematics 
title: "Forward Kinematics"
keywords:

- Open-Chain
   - Forward
   - Kinematics
   - End-Effector
   - Robotics

Terms:

Forward Kinematics

  • Refers to the use of the kineamtic equations of a robot to compute the position of the end-effector from specified values for the joint parameters.

End Effector

  • Device at the end of a robotic arm designed to interact with the environment.

    • End effectors are typically the grippers of a robot

Denavit-Hartenberg Parameters

  • Referred to as D-H Parameters

  • Commonly used convention for selecting frames of reference to the links of a spatial kinematic chain

Product of Exponentials

  • Referred to as PoE

  • Adjacent frames do not need to be considered.

  • Only 2 frames are needed: Space Frame {s} and Tool Frame {b}

  • 6n numbers are needed to describe n screw axes

Forward Kinematics

  • Forward kinematics refers to the use of the kinematic equations of a robot to compute the position of the end-effector from specified values for the joint parameters.

Problem

Define a frame {s} (often fixed at the base of a robot) and a frame {b} at the end effector of the robot arm.

Calculate the Forward Kinematics of the robot: I.e., FindT(θ)Find \newline T(\theta)

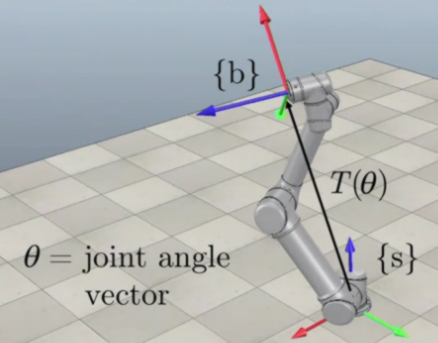
Representing Forward Kinematics in the {s} Frame

Procedure:

  1. Let M be the transformation matrix of the end-effector frame {b} when θ\theta = 0

    In other words, M is the position and orientation of the end effector when all joint angles are set to zero:

    xbybzbx_b\quad y_b\quad z_b\quadM=[xs^xs^xs^∑Lxsys^ys^ys^∑Lyszs^zs^zs^∑Lzs0001]M = \begin{bmatrix} \hat{x_s} & \hat{x_s} & \hat{x_s} & \sum{L}_{x_s} \\ \hat{y_s} & \hat{y_s} & \hat{y_s} & \sum{L}_{y_s} \\ \hat{z_s} & \hat{z_s} & \hat{z_s} & \sum{L}_{z_s} \\ 0 & 0 & 0 & 1 \end{bmatrix}

    • The first three 3-vectors (x,y,z) denote which axis in the {s} frame corresponds to a value in the {b} frame. For example, a value of [0,1,0]T[0, 1, 0]^T in the first column means that the x axis of the {b} frame is aligned with the positive y axis of the {s} frame

    • The bottom row is added to simplify matrix operations

    • The ∑L\sum{L} represents the sum of all of the links from the space frame {s} to the end effector.

  2. Find the {s} frame Screw Axes S1,...,SnS_{1}, ..., S_n for each of the n joint axes when θ=0\theta = 0

    Sn=[ωv]=[xs^ys^zs^xs˙ys˙zs˙]S_n = \begin{bmatrix} \omega \\ v \end{bmatrix} = \begin{bmatrix} \hat{x_s} \\ \hat{y_s} \\ \hat{z_s} \\ \\ \dot{x_s} \\ \dot{y_s} \\ \dot{z_s} \end{bmatrix}

    • The first 3-vector (angular velocity) represents which axis the space frame {s} is rotating about. For example, a value of [0,0,1]T[0,0,1]^T means that this joint in the {s} frame is rotating about the positive z-axis

    • The linear velocity v can be found by identifying which axis is tangental to the turntable created at the center of the joint n and then multiplying that number with the distance that the joint is from the origin of the {s} frame.

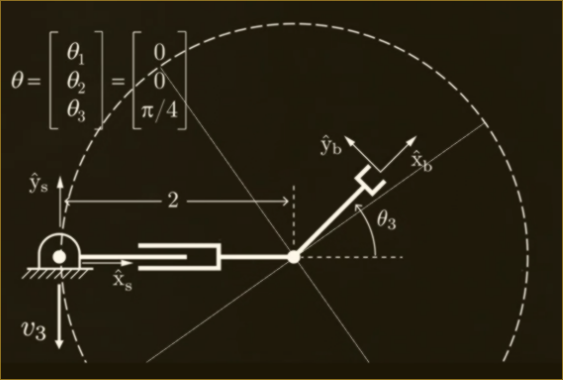
  3. Given θ\theta, calculate the product of exponentials (PoE) formula in the space frame:

    T(θ)=e[S1]θ1e[S2]θ2..e[sn]θnMT(\theta) = e^{[S_1]\theta_1}e^{[S_2]\theta_2}..e^{[s_n]\theta_n}M

Example:

Given a 4 joint RRRP Robot Arm, find the Forward Kinematics:

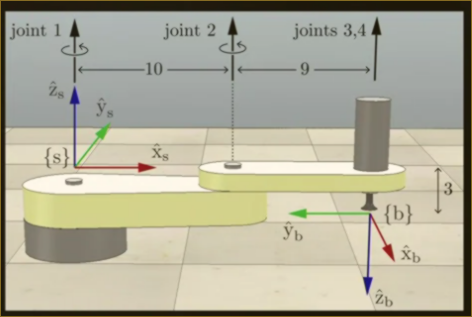
1st, Find M:

M=[0−1019−100000−1−30001]M = \begin{bmatrix} 0 & -1 & 0 & 19 \\ -1 & 0 & 0 & 0 \\ 0 & 0 & -1 & -3 \\ 0 & 0 & 0 & 1 \end{bmatrix}

2nd, Find all Screw Axes:

S1=[001000],S2=[0010−100],S3=[0010−190],S4=[000001]S_1 = \begin{bmatrix} 0 \\ 0 \\ 1 \\ \\ 0 \\ 0 \\ 0 \\ \end{bmatrix}, S_2 = \begin{bmatrix} 0 \\ 0 \\ 1 \\ \\ 0 \\ -10 \\ 0 \end{bmatrix}, S_3 = \begin{bmatrix} 0 \\ 0 \\ 1 \\ \\ 0 \\ -19 \\ 0 \end{bmatrix}, S_4 = \begin{bmatrix} 0 \\ 0 \\ 0 \\ \\ 0 \\ 0 \\ 1 \end{bmatrix}

Note, for S4S_4, the angular velocity is 0 because joint 4 is a prismatic joint which can only slide

3rd, that's it!

We now have the elements necessary to calculate the forward kinematic of the robot T(θ\theta) for any given theta

Representing Forward Kinematics in the {b} Frame

Procedure:

  1. Unchanged: Let M be the transformation matrix of the end-effector frame {b} when θ\theta = 0

    xbybzbx_b\quad y_b\quad z_b\quadM=[xs^xs^xs^∑Lxsys^ys^ys^∑Lyszs^zs^zs^∑Lzs0001]M = \begin{bmatrix} \hat{x_s} & \hat{x_s} & \hat{x_s} & \sum{L}_{x_s} \\ \hat{y_s} & \hat{y_s} & \hat{y_s} & \sum{L}_{y_s} \\ \hat{z_s} & \hat{z_s} & \hat{z_s} & \sum{L}_{z_s} \\ 0 & 0 & 0 & 1 \end{bmatrix}

  2. Find the {b} frame Screw Axes β\beta_{1}, ..., β\beta_n for each of the n joint axes when θ\theta = 0

    βn=[ωv]=[xb^yb^zb^xb˙yb˙zb˙]\beta_n = \begin{bmatrix} \omega \\ v \end{bmatrix} = \begin{bmatrix} \hat{x_b} \\ \hat{y_b} \\ \hat{z_b} \\ \\ \dot{x_b} \\ \dot{y_b} \\ \dot{z_b} \end{bmatrix}

    • The first 3-vector (angular velocity) represents which axis the space frame {b} is rotating about. For example, a value of [0,0,1]^T means that this joint in the {b} frame is rotating about the positive z-axis

    • The linear velocity v can be found by identifying which axis is tangental to the turntable created at the center of the joint n and then multiplying that number with the distance that the joint is from the origin of the {b} frame.

  3. Given θ\theta, calculate the product of exponentials (PoE) formula in the space frame:

    T(θ)=e[S1]θ1e[S2]θ2..e[sn]θnMT(\theta) = e^{[S_1]\theta_1}e^{[S_2]\theta_2}..e^{[s_n]\theta_n}M

Example:

Given a URRPR spatial open chain robot, determin the screw axis βi\beta_i in {b} when the robot is in its zero position. L = 1.

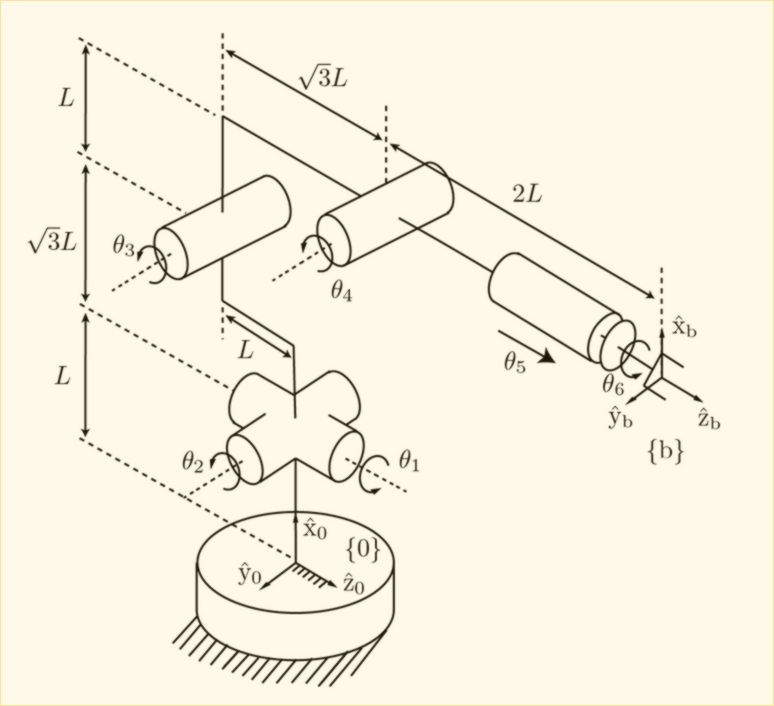
1st, Find M:

M=[1003.7301000012.730001]M = \begin{bmatrix} 1 & 0 & 0 & 3.73 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 2.73 \\ 0 & 0 & 0 & 1 \end{bmatrix}

2nd, Find all Screw Axes:

β1=[00102.730],β2=[0102.730−2.73],β3=[0103.730−1],β4=[010200]β5=[000001]β6=[001000]\beta_1 = \begin{bmatrix} 0 \\ 0 \\ 1 \\ \\ 0 \\ 2.73 \\ 0 \\ \end{bmatrix}, \beta_2 = \begin{bmatrix} 0 \\ 1 \\ 0 \\ \\ 2.73 \\ 0 \\ -2.73 \end{bmatrix}, \beta_3 = \begin{bmatrix} 0 \\ 1 \\ 0 \\ \\ 3.73 \\ 0 \\ -1 \end{bmatrix}, \beta_4 = \begin{bmatrix} 0 \\ 1 \\ 0 \\ \\ 2 \\ 0 \\ 0 \end{bmatrix} \beta_5 = \begin{bmatrix} 0 \\ 0 \\ 0 \\ \\ 0 \\ 0 \\ 1 \end{bmatrix} \beta_6 = \begin{bmatrix} 0 \\ 0 \\ 1 \\ \\ 0 \\ 0 \\ 0 \end{bmatrix}

Calculating the linear velocity looks complicated but is still quite simple. Take a look at θ1\theta_1. If you were to map that rotation onto the body frame {b}, you would notice that axis y is tangential to the rotation. It is also 2.73 units away from the {b} frame which is why it gets the value assigned.

Next, take a look at θ2\theta_2. It's rotation is tangential to both the x and z frames, so those will be assigned values. It is translated along the zbz_b axis by a unit of 2.73 and along the xbx_b axis by a unit of 2.73. The sign is produced from applying the multiplication formula: vi=−ωi×qiv_i = -\omega_i \times q_i. Here, -ωi\omega_i is (0,-1,0), which will invert the sign of the z axis.

Alternatively, you could just apply the formula for each vector to determine the linear velocity. Less error prone even though it takes more time.

3rd, that's it!

We now have the elements necessary to calculate the forward kinematic of the robot T(θ)T(\theta) for any given theta